Volume of a Octahedron
Volume calculator for a octahedron
Description, how many faces, edges and vertices are there in a octahedron
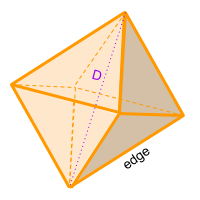
The octahedron, (Octa = 8 and Hedron = Face) is a solid that has 8 faces where each of these faces is an equilateral triangle, has 12 edges and 6 vertices. Also, the octahedron has 3 diagonals that join two vertices of different faces.
Note that the hexagonal prism also has 8 faces, so it could be called an octahedron, but the common way is to call it a hexagonal prism and the solid that we are analyzing is called an octahedron.
Examples of a octahedron
We can find many objects that look like an octahedron, examples of octahedron shaped objects are: 8-sided dice used in some board games; Another well-known object that has a very high monetary value is diamonds.Can you think of any other examples? leave a comment in the comment section at the bottom of the page.
Formula for the volume of a octahedron
To calculate the volume of an octahedron is very simple, you need to divide the square root of two by 3 and then multiply this result by the value of the edge powered to 3.
This solid is equivalent to having two square pyramids joined by their bases, so to get the volume you could consider the volume of the square pyramid that forms the octahedron and then multiply it by 2.
In case you don't know the value of an edge, but you do know the value of the diagonal (D), you can use the formula for the diagonal of an octahedron to calculate the value of the edge. The value of the edge is the value of the diagonal divided by the square root of two. You can also use the online calculator to calculate the volume of the octahedron automatically.
If you don't know the value of the edge, you can use the value of the Diagonal (D) of the octahedron:
Therefor, the edge value is calculated as:
As mentioned above, the octahedron can be formed by two square pyramids joint by the bases. The formula for the volume of a square pyramid is:
So, the double of the volume of a square pyramid is the same as the volume of an octahedron. If we express this into a formula we get (remember that the height mentioned below are the height of the pyramid):
Bear in mind that thanks to Pythagoras theorem, the height can be written as:
Replacing the height in the formula (1) we get the main formula:
Volume of other shapes
Volume of different geometric shapes:
